Guess My X/OG

Guess My X
Contributors	Yishay Mor
Last modification	May 15, 2017
Source	Mor (2008)
Pattern formats	OPR Alexandrian
Usability
Learning domain
Stakeholders

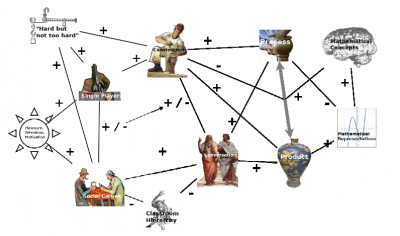
Use a Challenge Exchange (Challenge Exchange) game of Build This (Build This) puzzles to combine construction and conversation, promoting an understanding of process-object relationships and lead to meta-cognitive skills such as equivalence classes, proof and argumentation.

The problem

A teacher wants to design a game for learning concepts, methods and meta-cognitive skills in a particular mathematical domain. This game should use a combination of available technologies.

Many complex concepts require an understanding of the relationship between the structure of an object and the process which created it. Novices may master one or the other but find it challenging to associate the two. Constructing objects helps build intuitions, and discussing them espouses abstracting from intuitions and establishing socio-mathematical norms

Learning mathematics is fundamentally learning to be a mathematician. It requires the learner to internalize a range of mathematical skills as regular habits: computation, analysis, conjecturing and hypothesis testing, argumentation and proof. For this to happen, the learner needs to be deeply engaged in meaningful mathematical inquiry, problem solving and discussion. Games provide a natural setting for the kind of “flow” needed, but how do we ensure that the focus of this flow is mathematical activity and discourse?

Forces

Figure 1. Force map for the Guess my X design pattern

•Many mathematical domains require learners to understand the relationship between mathematical objects and the process which generated them. This is a challenge for many learners.

•The teacher needs a non-invasive monitoring mechanism to assess students' performance.

•The communicational approach sees learning mathematics as acquiring a set of language rules and meta-rules. In order to achieve this, learners need to engage in meaningful and sustained discussion of mathematical topics.

•The classroom hierarchies and the perception of a teacher as more knowledgeable causes learners to be cautious and restrained in their mathematical discourse.

Context

Primarily, a classroom supported by a technological environment which provides a shared and protected web space (e.g. wiki or forum), common tools (programming environment, spreadsheets, etc.) and sufficient access time for all students.

The game relies on sustained interaction over a period of several sessions. It can be used as a short introduction to a topic, but the greater meta-cognitive benefits may be lost if not enough time is allowed for conversations to evolve.

Also works for several groups collaborating over a web-based medium.

Solution

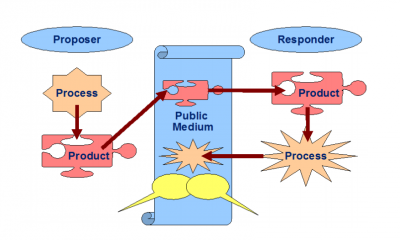
Guess my X (GmX) is a pattern of game structure, which can be adapted to a wide range of mathematical topics. It extends Challenge Exchange (Challenge Exchange) to encourage discussion and collaborative learning, and to break down classroom hierarchies. It uses Build This (Build This) to engender reflection and discussion about the relationships between mathematical objects and the processes that produce them. The core of the pattern is described in Figure 2.

Figure 2. Schematic diagram of GmX

GmX involves players in two roles, proposers and responders, and a facilitator. An implementation of the game would specify a domain of mathematics and rules for constructing processes in that domain. A proposer sets a challenge, in the form of a mathematical object which she constructed. The explicit rules of the game define the nature of the process by which this object can be created, but not its details. A proposer would construct such a process, and capture its product. The proposer then saves the process model in a private space and publishes the product as a challenge. Responders then need to “reverse engineer” the process from the product. If they succeed, they publish their version as a response to the challenge. The proposer then needs to confirm the responder’s solution of provide evidence for the contrary.

It is important to keep the mathematical content explicit from the start. The game is not a Sugar-Coating (Sugar-Coating) to disguise the mathematics: it is a game with Mathematical Game Pieces (Mathematical Game Pieces). The rules of the game are intentionally left vague, in the sense that the evaluation function used to determine the responders' success is not fully specified. This requires students to negotiate what constitutes a correct answer, and in doing so collaboratively refine the underlying mathematical concepts. These negotiations can lead to discussions of issues such as proof, equivalence and formal descriptions. The quality and extent of these discussions depends on the scaffolding and provocations provided by the teacher, but a necessary condition for them to emerge is that the medium of the game provide a Narrative Spaces (Narrative Spaces), Where the Mathematical Game Pieces (Mathematical Game Pieces) of the game can become Objects to Talk With (Objects to Talk With).

Set-up phase

Before the game begins, the teacher needs to verify that the players have a minimal competence in analysing and constructing the mathematical objects to be used.

1. Teacher introduces the rules of the game and the game environment.

2. Teacher simulates one or two game rounds during a whole class discussion.

3. Students may need to initialize their game space on the chosen collaborative medium.

If the game uses separate media for construction and communication, consider using a Task In A Box (Task In A Box) to streamline the transition between them.

Game session

The game sessions for the proposer and the responder are different, although the same player can play both parts in parallel.

1. Proposer initiates the game, by constructing and object according the game rules and publishing it. She then waits for responses.

2. Responder chooses an attractive challenge, and attempts to resolve it. If she believed she has succeeded, she responds to the challenge by posting the object she constructed and the method she used.

3. Proposer reviews the response, and confirms or rejects it. If the response is rejected, an argument needs to be provided.

Play session

Each play session involves a single iteration of the game. Students tend to prolong their interaction in the game, by providing secondary challenges, etc. Since the iterations are a-synchronous, there may be a time gap of several days between turns.

The communication medium chosen for the game should afford Narrative Spaces (Narrative Spaces) for the proposer and the responder. Although the rules of the game are limited to the exchange of mathematical objects, the ability to augment these with personal narratives is crucial for personal reflection as well as for collaborative knowledge building.

Set-down phase

The Post Ludus (Post Ludus) discussion should highlight the issue of the evaluation function and its resolution.

Examples

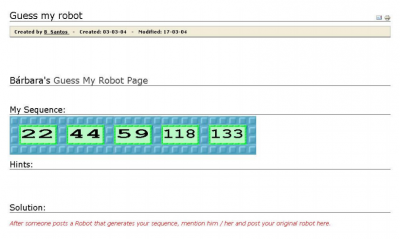
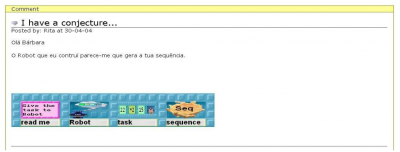
In the Guess my Robot game students exchanged challenges in the domain of number sequences. Proposers would program a ToonTalk robot to produce a sequence, keep the robot to themselves, and publish the first few terms of the sequence (Figure 3). Responders would then solve the challenge by recreating a robot to produce the same sequence and posting it as a comment on the challenge page (Figure 4). Often the response robot was different from the original, which led learners to discussions about issues such as proof and equivalence. The same structure was then used in the Guess my graph game in the domain of function graphs and the Guess my garden game in the domain of randomness and probability.

Figure 3. Example of guess my robot challenge

Figure 4. Example of guess my robot response

Related Patterns

Elaborates: Mathematical Game Pieces (Mathematical Game Pieces)

Uses: Challenge Exchange (Challenge Exchange); Undercover Process (Undercover Process); Build This (Build This); Task In A Box (Task In A Box); Objects to Talk With (Objects to Talk With); Narrative Spaces (Narrative Spaces)

Leads to: Post Ludus (Post Ludus)

Notes

Guess my X assumes a degree of social and technical sophistication which suggests it would be suitable for young teens and above. It can, however, be adapted for younger children.

The game requires flexibility in time to allow learning dynamics to emerge. It can be interleaved with other activities.

It is suitable for concrete, well-bounded content domains, such as computation, modelling or analysis. It uses these as a stratum for developing meta-cognitive skills of problem solving, analysis, argumentation and general mathematical discourse.

The fact that the game dynamics are driven by participants makes the educators’ role subtle and critical. The educator needs to facilitate fruitful interactions, and monitor these to divert them to high standards of mathematical discourse.

The game can be played by individuals, pairs or teams. The number and spread of participants can also vary. However, it is crucial to allow enough time for a culture to emerge. This can be achieved by interleaving the game with other activities, e.g. playing it for the last 10 minutes of each session over several weeks.

Both proposers and responders tend to converge to challenges which are Hard But Not Too Hard (Hard But Not Too Hard). When the environment encourages social cohesion, players seem to reciprocate 'good' challenges.