Hint on Demand/OG
| Hint on Demand | |
| Contributors | Marc Zimmermann, Daniel Herding, Christine Bescherer |
|---|---|
| Last modification | May 15, 2017 |
| Source | Zimmermann, Herding & Bescherer (2014)[1] |
| Pattern formats | OPR Alexandrian |
| Usability | |
| Learning domain | |
| Stakeholders | |
Students in mathematical courses at university have to work on weekly exercises in addition to attending lectures. Most of these exercises can be solved by performing several discrete steps, but for students they can seem complex and many of them have difficulties in carrying out these exercises. These difficulties can usually be overcome by hints given by a tutor, but students working alone cannot get access to this support. Similarly, tutors cannot provide this support to students in large classes. In this pattern, the proposed solution is to make hints accessible in a semiautomated way. Hints for expected mistakes, or on notation problems, will be given automatically. Hints for specific individual problems will be given by the tutor. The hints are given when the learner actively demands them and not before he/she has started working on the task.
Problem
In many subjects at university students have to work on weekly exercises to practice what they have learned in addition to attending lectures. Students will follow different approaches in the use of solution processes even though the tutor may have a clearly intended goal for the exercises. These exercises, which have several different possible solutions, can seem difficult and complex, in particular for students in introductory courses. Many students avoid working on a task after a first glance because they think that they cannot handle it. Every task that cannot be solved decreases the student’s motivation and reinforces a negative attitude towards the subject. In many cases, one or a few hints at the right time would suffice to enable the student to master the task.
In face-to-face situations like tutorials, open learning scenarios such as tutors’ office hours[2]or small courses, lecturers or tutors can immediately offer clues or hints on the students’ solution processes. They can directly intervene when they see that students get stuck. In contrast, when the learners are on their own, e.g. working at home, or in a course with many participants, there is hardly any possibility to get prompt hints on the solution process. Lecturers could offer hints on expected difficulties to students before they start working on the exercises, but this strategy has some disadvantages. Firstly, good students are able to solve the exercise without any hints; providing hints at the beginning would bore them or even keep them from working on the task. Too much of the solution could be revealed beforehand by these hints, making the exercise too easy for them. Secondly, novices usually cannot remember a large number of hints, and they may get confused by too many hints if they haven’t experienced the problem yet. In addition, weak students may need assistance during the solution process to make up a solution in the first place, while good students may need hints afterwards on minor mistakes such as use of incorrect notation.
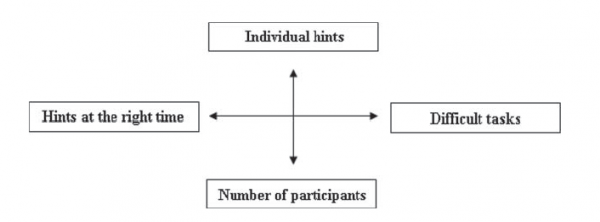
Forces
The forces in tension in this pattern are:
– Number of participants: In introductory courses with a high number of participants, giving hints to each student takes too much of the lecturers’ or tutors’ time. Many of the students’ problems are common problems, thus similar hints have to be given many times.
– Individual hints: Good students may be able to solve the problem on their own without any additional hints other than on minor issues of notation etc. Other students may need assistance to develop a solution in the first place. Furthermore, most learners first have to realize that there is a problem before they can recognise a hint as helpful.
– Difficult tasks: At first view, a mathematical task may seem unsolvable for many students. Without clues, they quit working early or even refrain from trying to solve the task in the first place. This can lead to a decrease in motivation for mathematical tasks and in the students’ mathematical self-efficacy expectations.
– Hints at the right time: Tutors often give numerous hints before the learner has worked on the task in order to avoid expected difficulties. However, novices usually cannot remember a large number of hints, or may even get confused by them. For good students, revealing too much of the solution beforehand can make working on the task too easy and possibly boring.
Context
Hints can be given in every situation in which a learner is at a loss, for example when they have arrived at an incorrect solution, when they get stuck, or when they don’t know how to get started. Hints help learners to start or to continue working on exercises. Even though this pattern can be transferred to other subjects, we will concentrate on mathematics, as this subject is a component of many study courses such as medicine, computer science, and psychology.
In mathematics courses at university, students have to solve weekly exercises and hand them in to the lecturer or tutor. Most of the exercises can be solved by performing several discrete steps, such as transforming a term, substituting a variable, or drawing a triangle. Weaker students often get stuck on one of these steps, and some of them simply copy the solution from better students. Their understanding of mathematics decreases, and mathematics become a mystery to them.
In computer-based tasks or learning scenarios in mathematics, the situation is quite similar. As students work on computer-based exercises, problems can occur during the solution process. Many e-learning applications only provide help on the functions of the application, but not on the problems that may occur. As a consequence, the learner puts off working on the task, and the motivation to work with e-learning applications in general can decrease.
Solution
Exercises can be differentiated into objective and non-objective tests[3]. In objective tests, such as multiple-choice tests with only one correct solution, hints can help the learner to recall the necessary knowledge. Hints for objective tests are easy to give as the solution space is narrow, so we will not concentrate on these kinds of tasks. Most mathematical tasks, however, are nonobjective because there are a great number of possible correct solution processes. For example, there are several ways of proving a mathematical theorem, and the tutor cannot predict how the students will approach the exercise. In our solution, hints can be accessed in a semi-automatic way. Learners working on their own can get access to hints any time.
Hints on frequently asked questions or frequently described problems (e.g. hints on format, notation, or orthography) should not be given in the lecture or attached to the assignment sheets. Weaker students would get confused, as they cannot relate these hints to the exercises. Such hints can be prepared beforehand and deposited in online forums or Learning Management Systems (LMS) in a way that the learner can fetch them when he/she requires them. Students can access these ‘automated’ hints at any time during their solution process once they have explored the problem space, so that the hint can better be anchored with regards to the content, making it possible for the student to reflect upon his/her solution process. Ideally, the learner will have attempted several (ineffective) solution steps before asking for a hint. In order to increase the learner’s performance on the task, hints should be given at different levels. For example, access to a more detailed hint should only be provided if less detailed hints have been read before. Unusual or quite specific hints still have to be given by the tutor in person. Learners have to write an email or talk to the lecturer or tutor by phone or in face-to-face tutorials. Because tutors need not concentrate on common questions or problems, they have more time for unusual solutions and weaker students.
Computer-based exercises can ease the tutorial work by giving feedback to standard solutions and mistakes[4]. They use intelligent assessment algorithms to evaluate each solution step with regard to different criteria. These tools can be extended so that an additional hint is available for each feedback message. This hint function has to be limited in a way that prevents students from solving the task by just requesting a hint for each solution step[5]. This restriction can be realized by limiting the number of hints a student can request per exercise. For more detailed or specific hints, students can contact their tutor.
Support
Source
The source for the pattern Hint on Demand (Hint on Demand) is the design narrative ‘A learning tool for mathematical proofs with on-demand hints’[6], which describes one of the tools developed in the SAiL-M project (Semi-automatic Analysis of individual Learning Processes in Mathematics, funded by the Federal Ministry of Education and Research (BMBF) from 10/2008 to 02/2012). When the learner uses a tool like ColProof-M, he/she can take hints to complete or to improve his/her solution.
Supporting Cases
The interactive geometry software Cinderella[7] incorporates an intelligent tutoring system. When doing an exercise using this tool, students can ask for a hint. The software then decides, based on the constructed geometric objects, which hint could be adequate and in which way it should be given. The software only uses a single reference solution for comparison with the learners’ partial solution. This approach is described by Müller et al.[8] and by Bescherer et al.[9].
The OU Exercise Assistant[10] is another e-learning tool in which students have to reduce propositional expressions. After each transformation entered by the user, a system checks the solution step and automatically provides feedback whether the solution is correct or incorrect. If the learner does not know the next transformation step, he/she can either request a hint or ask for the entire next step. In this case, it is possible to finish the exercise via the auto-step function. When students work on mathematical problems, students need individual and just in-time help[11]. Students can then continue working on the problem without losing too much motivation and time. In our context, the term ‘help’ could equally be understood in the sense of ‘hints’.
Giving hints on different levels of detail is an idea described by Wood and Wood[12]. The theory of contingent tutoring indicates that tutors should give hints related to the learner’s problems. When the first hint does not lead to success, the tutor has to give a more detailed, or more explicit, hint. The first level of hints can be questions which point to a possible solution, e.g. ‘Did you already try XY?’ or ‘Think about a way you can also reach XY!’ Further levels of hints can be more precise and contain explicit advice.
Guiding the students’ solution processes relies on the ‘scaffolding’ teaching method of the cognitive apprenticeship model[13] A tutor supports the solution process of the students by giving help or hints. A scaffold to solve the task can be built for the students, who can use it to solve the problem. The support can be reduced (‘fading’, ibid: p.482) when the students have fewer problems. Similarly, in our concept, students work on exercises to practice their understanding of the contents of the lectures. When students get stuck, tutors can give more or less detailed hints which allow the learners to finish their individual solutions.
Verification
In the SAiL-M project, we worked with an unusual philosophy of introductory courses for mathematics. At the University of Education in Ludwigsburg, students did not have to hand in weekly tasks for assignment. Tutors also did not give ‘the correct’ solution, and students were not required to present their solution in tutorials. Instead, they worked on the weekly exercises in small groups supported by tutors. The tutors guided the students by giving hints or asking questions about the exercises. This encouraged the students to reflect on their actions. This constructivist approach is described in the Activating Students in Introductory Mathematics Tutorials (Activating Students in Introductory Mathematics Tutorials) pattern by Bescherer et al.[14]
Related patterns
– Technology on Demand (Technology on Demand)[4]: Students should be able to use software for solving problems whenever they think it will be useful. They have to learn when to use which software in which context.
– Help on Demand (Help on Demand)[4]: When students use software to solve a task, they often need help regarding the technical use of the application. These difficulties can distract them from the learning contents. An on-demand help function can help students to stay focussed on the mathematical problem.
– Feedback on Demand (Feedback on Demand)[4]: Students should be able to get process-oriented feedback when they need it even in courses with many participants. Lecturers should also be able to select interesting (correct or incorrect) solutions for discussion of mathematical processes in the lectures.
– Try Once, Refine Once (Try Once, Refine Once): Students should be able to resubmit a corrected version after getting feedback on their initial answers.
– Feedback on Feedback (Feedback on Feedback): Tutors need to receive feedback on their own feedback. This is also true for hints they give. Also, the feedback and hints that are automatically generated by e-learning applications must be evaluated and improved.
– Blended Evaluation (Blended Evaluation): Hints can come from different sources, e.g. from peers, from tutors, or automatically generated from tools.
References
- ↑ Zimmermann, M., Herding, D. & Bescherer, C. (2014). Pattern: Hint on Demand. In Mor, Y., Mellar, H., Warburton, S., & Winters, N. (Eds.). Practical design patterns for teaching and learning with technology (pp. 329-335). Rotterdam, The Netherlands: Sense Publishers.
- ↑ Zimmermann, M. (2012). Der offene Matheraum als Baustein für aktives Mathematiklernen. In Zimmermann, M., Bescherer, C. & Spannagel, C. (Eds.), Mathematik lehren in der Hochschule– Didaktische Innovationen für Vorkurse, Übungen und Vorlesungen. Hildesheim, Germany: Franzbecker.
- ↑ Bull, J., & McKenna, C. (2004). Blueprint for computer-assisted assessment. London: Routledge.
- ↑ 4.0 4.1 4.2 4.3 Bescherer, C., & Spannagel, C. (2009). Design patterns for the use of technology in introductory mathematics tutorials. In Education and technology for a better world (pp. 427-435). Springer Berlin Heidelberg.
- ↑ Aleven, V., & Koedinger, K. R. (2000). Limitations of student control: Do students know when they need help? In Gauthier, C.F.G. & VanLehn, K. (Eds.), Proceedings of the 5th International Conference on Intelligent Tutoring Systems (ITS 2000). Springer Berlin Heidelberg.
- ↑ Herding, D., Zimmermann, M. & Bescherer, C. (2014). Design Narrative: A Learning Tool for Mathematical Proofs with On-Demand Hints. In Mor, Y., Mellar, H., Warburton, S., & Winters, N. (Eds.). Practical design patterns for teaching and learning with technology (pp. 285-291). Rotterdam, The Netherlands: Sense Publishers.
- ↑ Richter-Gebert, J., & Kortenkamp, U. (2012). The Cinderella 2 manual. Berlin, Heidelberg: Springer.
- ↑ Müller, W., Bescherer, C., Kortenkamp, U., & Spannagel, C. (2006). Intelligent computer-aided assessment in math classrooms: State-of-the art and perspectives. Alesund, Norway: Paper presented at IFIP WG 3 Conference on Imagining the future for ICT and Education. Retrieved December 24, 2012, from http://www.ph-ludwigsburg.de/fileadmin/subsites/2e-imix-t-01/user_files/personal/spannagel/publikationen/Mueller_et_al_-_Intelligent_Computer-Aided_Assessment.pdf.
- ↑ Bescherer, C., Herding, D., Kortenkamp, U., Müller, W., & Zimmermann, M. (2012). E-learning tools with intelligent assessment and feedback for mathematics study. In Intelligent and adaptive learning systems: Technology enhanced support for learners and teachers. Hershey, PA: IGI Global.
- ↑ Heeren, B., Jeuring, J., & Gerdes, A. (2010). Specifying rewrite strategies for interactive exercises. Mathematics in Computer Science, 3(3), 349–370.
- ↑ Ames, A. L. (2001). Just what they need, just when they need it: an introduction to embedded assistance. In Communicating in the New Millenium. Proceedings of the 10th Annual International Conference on Systems Documentation. ACM.
- ↑ Wood, H., & Wood, D. (1999). Help seeking, learning and contingent tutoring. Computers and Education, 33(2–3), 153–169.
- ↑ Collins, A., Brown, J. S., & Newman, S. E. (1989). Cognitive apprenticeship: Teaching the crafts of reading, writing, and mathematics. In Resnick, L. B. (Ed.), Knowing, learning, and instruction: Essays in honor of Robert Glaser (p.428). Hillsdale, NJ: Erlbaum.
- ↑ Bescherer, C., Spannagel, C., & Müller, W. (2008). Pattern for introductory mathematics tutorials. In Proceedings of the 13th European Conference on Pattern Languages of Programs (EuroPLoP 2008). New York:ACM. Retrieved November 3, 2011, from http://ceur-ws.org/Vol-610/paper17.pdf.