Image-Enhanced Problem
| Image-Enhanced Problem | |
| Contributors | Paul Salvador Inventado, Peter Scupelli |
|---|---|
| Last modification | May 17, 2017 |
| Source | Inventado and Scupelli (2016).[1] |
| Pattern formats | OPR Alexandrian |
| Usability | |
| Learning domain | |
| Stakeholders | |
Clarify ambiguous terms and explanations in the math problem by adding appropriate images.
Context
A problem-solving activity is being designed for an online learning system to help students understand a topic they recently learned.
Problem
Students are unable to solve some problems that contain ambiguous terms and explanations.
Forces
- Term familiarity. Some terms may have multiple meanings. Students may interpret a term the way they are most accustomed to, which can be different from the intended use. In some cases, students may not understand the term at all.
- High cognitive load. Students’ cognitive load increase when they try to comprehend ambiguous terms and explanations aside from understanding and solving a problem.
- Time. Students may spend more time trying to understand the problem instead of solving it.
- Misunderstanding the problem. Students may end up solving for something unrelated if they misunderstand the problem.
- Unnecessary information. Providing elaborate explanations to clarify terms make the problem longer and can distract students from the actual problem.
Solution
Therefore, provide simple images and reference them in written text to clarify ambiguous terms and explanations. Do not add unnecessary details in images that may distract students from the focus of the problem or reveal learning objectives. Place the image close to the section of the written text that references it so that students do not need to scroll up and down the screen.
Consequences
Benefits
- Images can succinctly illustrate concepts that may clarify and disambiguate confusing terms and explanations.
- Students can focus their mental effort on solving the problem after they disambiguate terms and explanations.
- Clear and simple images can help students understand the problem quickly, which leaves them more time to solve it.
- Students are less likely to solve for something unrelated when they have a clear understanding of the problem.
- Well-designed images can express ideas concisely that will allow students to focus on the important elements of the problem.
Liabilities
- It takes more time and effort to create appropriate images for each problem.
- Some ideas, such as abstract concepts, are difficult to illustrate.
- Images take a longer time to load over the network compared to text.
- Images may not always appear on the screen as intended due to uncontrollable factors (e.g., screen size, color and screen resolution supported, image loading is disabled in the browser).
Evidence
Literature
- Long descriptive text can be expressed concisely with an image[2]
- Introducing unnecessary information and tasks increases cognitive load, which may make the task more difficult and less likely to be completed[3].
- The multimedia principle suggests the use of well-designed graphics and text to enhance understanding and learning[4][5].
Related patterns
The Image-Enhanced Problem design pattern can be used to clarify math problems that contain many details, which are easily confused. It can be used with the Representation Practice design pattern to provide students with essential images that can help clarify the problem without revealing too much information. Remember to use the Keep It Simple design pattern[6] when designing images so that unnecessary details do not distract students.
Provide facilities such as those described in the Represent It and Image-Enhanced Hint design patterns to help students who still struggle to solve the problem. The use of images to facilitate understanding and hints to support student learning may help maintain student motivation as described in the Build and Maintain Confidence design pattern[7].
Example
Learning systems often use images to clarify written problems. Higher learning gains were observed when images and text were used to present problems compared to text alone on different domains such as Mathematics[8][9], Biology [10], and reading and comprehension[11].
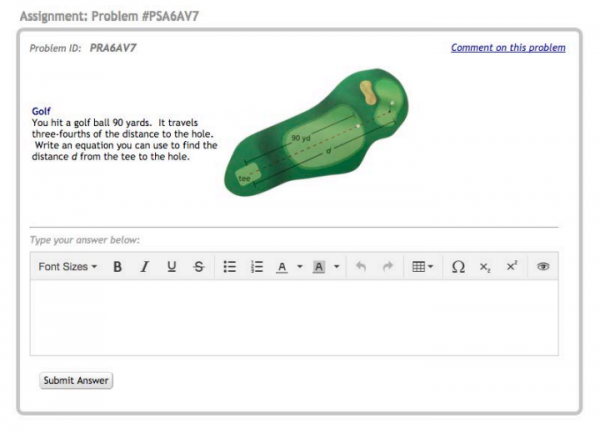
The figure below shows a math problem for writing equations. The problem uses a golf-analogy and introduces the terms “tee” and “hole”, which may be unfamiliar to some students. An image was used to illustrate the different problem elements, which may help students understand unfamiliar terms.
References
- ↑ Inventado, P.S. and Scupelli, P. (2016). Design Patterns for Helping Students to Learn to Visualize Math Problems in Online Learning Systems. In Proceedings of the 21st European Conference on Pattern Languages of Programs (EuroPLoP 2016). New York:ACM.
- ↑ Moyer, D. (2010). Just Show It. The napkin sketch workbook. Blurb.
- ↑ Sweller, J. (2004). Instructional design consequences of an analogy between evolution by natural selection and human cognitive architecture. Instructional science, 32(1-2), 9-31.
- ↑ Clark, R. C., & Mayer, R. E. (2016). E-learning and the science of instruction: Proven guidelines for consumers and designers of multimedia learning. John Wiley & Sons.
- ↑ Fletcher, J. D., and Tobias, S. (2005). The multimedia principle. In R.E. Mayer (Ed.), The Cambridge handbook of multimedia learning (pp. 117-134). New York: Cambridge University Press.
- ↑ Cunningham and Cunningham Inc. (2014). Keep it Simple. Retrieved from http://c2.com/cgi/wiki?KeepItSimple.
- ↑ Bergin, J., Eckstein, J., Völter, M., Sipos, M., Wallingford, E., Marquardt, K., Chandler, J., Sharp, H., and Manns, M.L. (2012). Pedagogical patterns: advice for educators. Joseph Bergin Software Tools.
- ↑ Heffernan, N.T. and Heffernan, C.L. (2014). The ASSISTments Ecosystem: Building a Platform that Brings Scientists and Teachers Together for Minimally Invasive Research on Human Learning and Teaching. International Journal of Artificial Intelligence in Education 24(4), 470-497.
- ↑ Moreno, R., & Mayer, R. E. (1999). Multimedia-supported metaphors for meaning making in mathematics. Cognition and instruction, 17(3), 215-248.
- ↑ Stull, A. T., & Mayer, R. E. (2007). Learning by doing versus learning by viewing: Three experimental comparisons of learner-generated versus author-provided graphic organizers. Journal of educational psychology, 99(4), 808.
- ↑ McCrudden, M. T., Schraw, G., & Lehman, S. (2009). The use of adjunct displays to facilitate comprehension of causal relationships in expository text. Instructional Science, 37(1), 65-86.